|
1. INTRODUCTION
There is a well-known lack of communication among physicists, ecologists, and economists.
Using a new framework of economic analysis, Concordian economics [1], a system of thought
that results from the relentless application of age-old tools of logic and epistemology to mainstream
economic theory, this paper attempts to build bridges among the various disciplines so that lines
of communication can be opened and solutions can be found to today’s vexing problems of
economics and ecology. Physicists, being practical problem solvers, and ecologists, being deeply
concerned about the status quo, might join together in this mission to let economics reach the
splendor of its full potential.
2. PROBLEM STATEMENT
Lack of communication among physicists, ecologists, and economists is rooted in the
practice of economists, who have developed their own specialized form of mathematics to analyze
economic problems; and have reduced the number of admissible problems to those that exist
in the market at the moment of the exchange. Thus they analyze only flows, not stocks of wealth;
and they observe only money, not real resources. In particular, physicists have long remarked that
modern economic theory cannot possibly be a fit description of the reality because, among other
reasons, it is a closed system without inlets and outlets [2]. Ecologists, on their part, never seem to
engage economists because, among other reasons, while they are mainly concerned with
stocks of real wealth, economists are mainly concerned with flows of money [3].
3. FINDINGS
Three essential findings of Concordian economics are reported here with the assistance of modern
mathematics and geometry: stocks are separated from flows of wealth; the real economy is
separated from the monetary economy; these two parts of the economic process are then joined
together through the introduction of the legal and institutional economy into the equations.
Through painstaking analysis (Gorga 2002, 23-158) [4], real wealth (RW) is defined as stocks of
consumer goods (CG), plus capital goods (KG) and goods hoarded (GH). The fundamental model
of production (P) is formulated as follows (Ibid., 38, 313):
P = CG + KG + GH
IA = P – GH
IA = (CG + KG)
where IA = Investment Assets (until sold). Monetary wealth (MW) is defined as the sum of all
financial instruments used to purchase CG, KG, and GH as well as other financial instruments:
corresponding equations form the model of consumption (Ibid., 318). The legal economy is
defined as the value of all rights of ownership over real and monetary wealth: corresponding
equations form the model of distribution (Ibid., 316). Since the structure of these models is selfsimilar,
they are omitted here.
The three systems of equations form an equivalence [5], the equivalence of production to
distribution and to consumption. They describe the same entity, the economic process, from three
strictly interconnected points of view. In more detail, this equivalence refers to the production of
all real wealth; the distribution of ownership rights over both monetary and real wealth; and
consumption (or expenditure) of monetary instruments to purchase real wealth. This
equivalence can be more easily observed with the assistance of geometry. Thus, using established
protocols, it is possible to synthesize the above three systems of equations into one unit
represented by the following diagram:
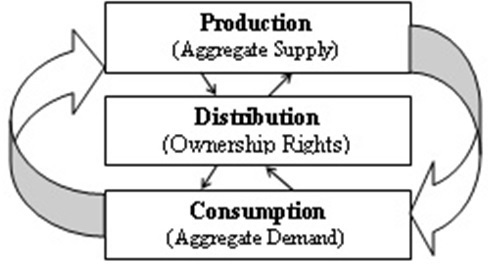
Figure 1 – The Economic Process
Figure 1 represents the economic process at the moment of the exchange—as in mainstream
economics, but with an enlarged focus. The unit of account can be the economy of an individual
person, an individual firm, the local, the national, or the world economy. Figure 1 reads as follows:
When goods and services pass from producers to consumers, monetary instruments of a
corresponding value pass from consumers to producers. For the exchange to occur, the
transactors must be the owners of both money and real wealth. Then, one cycle of the economic
process is completed. As can be seen, Concordian economics is wholly relational and
inherently dynamic. This second characteristic becomes more explicit if one sees each rectangle
of Figure 1 as a Poincaré section. In Figure 1 the economic process is observed at one static
moment in time.
There are three approaches for a comprehensive study of the dynamics of the
economic process. One is the analytical/mathematical approach. It yields the
following generalized system of equations:
p. = fp(p,d,c)
d. = fd(p,d,c)
c. = fc(p,d,c)
where p. = rate of change in the production of real wealth, d. = rate of change in the pattern of distribution of ownership rights over real and monetary wealth, and c. = rate of change in the
consumption or expenditure of monetary wealth.
The second approach for the study of the dynamics of the economic process is the
historical/latitudinal one. This study calls for following the dynamic transformation of the
system, ideally from the beginning of time till today. Starting from flows of real and monetary
wealth one obtains a result that is very familiar to modern physicists, a strange attractor or a Lorenz
attractor, see, e.g., Thompson (1986, 228) [6]. A few cycles are reproduced here:
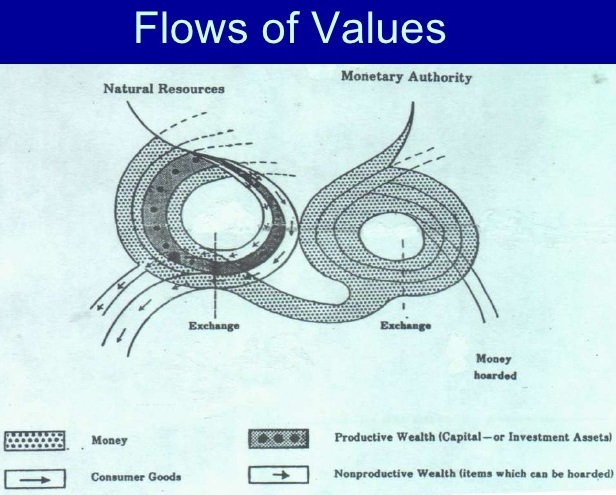
Figure 2 – Flows of Values
With Figure 2, we are not only within the economic process—an area that is a black box to
mainstream economics [7]; we have also found the inlets and outlets requested by physicists. The
inlets are flows of real and monetary wealth; the outlets are consumer goods, goods hoarded, and
money hoarded. It is only capital goods and money to purchase real wealth that remain
permanently within the system. The flows of the legal/institutional economy are fully inserted in this
construction: They are invisibly present at the moment of the exchange. In order to buy and sell
wealth one has forever had to have ownership of that wealth. Indeed, to think of the extreme
complexity of the reactions that occur within the economic system, the reader is encouraged to
mentally close the two halves of Figure 2 thus creating the image of a torus or a cyclotron. In the
reality of daily life, stocks and flows of real and monetary values do not organize themselves into
neat patterns, but tend to intermingle and interact with each other.
The third approach is the longitudinal/programmatic one, through which one
obtains an external view of the economic system as a whole.
This is a new perspective that yields a simplified understanding of other characteristics of
the economic system. This mode of analysis can be briefly described as follows: If the economic
system were composed of three identical, synchronous, and compenetrating spheres
(obtained by rotating each rectangle of Figure 1 at ever increasing speed and in all directions about
their geometric center), the system would leave behind only one trajectory as an indication of its
dynamics. This line—whatever its pattern—would indicate that the three spheres were in continuous
equilibrium with each other. This is not the case in economics: As Mandelbrot (1983, 1) [8] is fond of
saying, "Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is
not smooth, nor does lightning travel in straight lines." Can economic systems be expected to be
represented by perfect solids?
To say the least, the trajectory of aggregate values of monetary
wealth (MW) can be expected to soon leave the initial condition of equilibrium (0,0,0) and, spurred
by the facility with which monetary instruments can be produced, grow at a faster rate than the
trajectory of values of real wealth (RW). Also, the spheres representing the pattern of distribution of
values of ownership rights over real and monetary wealth, which are known to remain rather static
over time, can be conflated into two overlapping straight lines to be identified as DO. Then, over
time, eliminating all short and long term, cyclical, random, or aperiodic loops, breaks, and turns, the
system as a whole can be expected to leave behind idealized traces of motion as in the following figure:
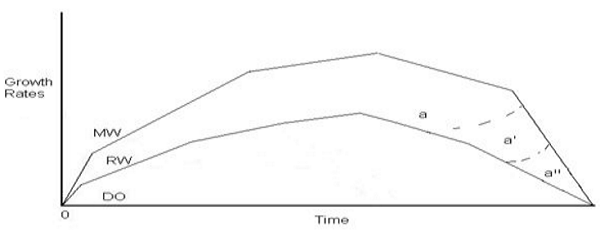
Figure 3. Trajectories of the System as a Whole
The distance between RW and MW will eventually yield the mathematical measurement of the
“bubble”. Current efforts to identify the bubble are especially intense [9]; physicists adept at chaos
theory have been investigating this issue for quite some time [10]. Area "a"—with its alternative subareas
a' and a''—attempts to describe the condition of disequilibrium (the bubble) that so
often develops between monetary and real wealth and suggests that the smaller this area, the
smaller the loss of real income over time. How to close the gap between the real and the monetary
economy in the shortest possible time is clearly a problem of control, namely, a problem of economic
policy—the problem of creating a just and sustainable economy.
4. CONCLUSION
There is much work to be done. As can be seen, the intellectual framework is mostly done; it is the
practical work that is all to be done. This is the work of organizing the data in accordance with the
categories of thought specified above; this is the work of analyzing the data with the assistance of
modern tools of scientific research. The tempi for the performance of this work can be enormously
speeded up if physicists, ecologists, and economists assiduously work together [11].
REFERENCES
[1] Gorga, C. (forthcoming), “Concordian economics: Tools to return relevance to
economics,” Forum on Social Economics.
[2] Nadeau, R. L., The Environmental Endgame: Mainstream Economics,
Ecological Disaster, And Human Survival, Piscataway, NJ: Rutgers University Press, 2006.
[3] Daly, H. E., Bouckaert, L., Opdebeeck, H., and Zsolnai, L., Frugality: Rebalancing
Material and Spiritual Values in Economic Life, Oxford, Bern, Berlin, Bruxelles,
Frankfurt am Main, New York, Wien: Peter Lang; pp. 207-226, 2008.
[4] Gorga, C., The Economic Process: An Instantaneous Non-Newtonian Picture,
University Press of America, Lanham, Md., and Oxford, 2002.
[5] Gorga, C., “On the Equivalence of Matter to Energy and to Spirit,” Transactions on
Advanced Research Vol. 3, N. 2: 40-45, 2007.
[6] Thompson, J. M. T., Nonlinear Dynamics and Chaos, Geometric Methods for
Engineers and Scientists, New York: Wiley, 1986.
[7] Petrongolo, B., Pissarides, C. A., “Looking into the Black Box: A Survey of the
Matching Function,” Journal of Economic Literature, Vol. XXXIX: 424, 2001.
[8] Mandelbrot, B. B., The Fractal Geometry of Nature, New York: W. H. Freeman, 1983.
[9] Because of its guidance from Ben Bernanke, most notable these days is the work done at
the Bendheim Center for Finance at Princeton (Princeton Weekly Bulletin, May 26, 1997 and ff.).
[10] See much work done at the Santa Fe Institute.
[11] Matthews, E., The Weight of Nations: Material Outflows from Industrial
Economies, Washington, D.C.: World Resources Institute, 2000.
|
ABOUT THE AUTHOR
Carmine Gorga is president of The Somist Institute. The mission of the institute is to foster sensible moral leadership. He is a former Fulbright scholar and the recipient of a Council of Europe Scholarship for his dissertation on “The Political Thought of Louis D. Brandeis.” By inserting Hoarding into Keynes’ model of the economic system and using age-old principles of logic and epistemology, in a book and a series of papers Dr. Gorga has transformed the linear world of economic theory into a relational discipline in which everything is related to everything else—internally as well as externally. He was assisted in this endeavor by many people, notably for 27 years by Professor Franco Modigliani, a Nobel laureate in economics at MIT. The resulting work,
The Economic Process: An Instantaneous Non-Newtonian Picture, was published in 2002 and has been reissued in a third edition in 2016. For reviews, click here. During the last few years, Dr. Gorga has concentrated his attention on the requirements for the unification of economic theory, policy, and practice calling this unity Concordian economics. He is also integrating this work into political science, which he calls Somism, and culture in general, which he calls Relationalism.
|
|